本文为转载文章
原文作者: MARK SHEAD
原文链接: State Machines – Basics of Computer Science
Computer science is what enables programming, but it is possible to do a lot of programming without understanding the computer science concepts underlying the process of computation. This isn’t always a bad thing. When we program we work at a much higher level of abstraction. When we drive a car, we only concern ourselves with two or three pedals, a gearshift, and a steering wheel. You can safely operate a car without having any clear idea of how it works. However, if you want to operate a car at the very limits of its capabilities, you need to know a lot more about automobiles than just the three pedals, gearshift and steering wheel.
The same is true of programming. Much mundane everyday work that can be accomplished with little or no understanding of computer science. You don’t need to understand computational theory to build a “contact us” form in PHP. However, if you plan to write code that requires serious computation, you are going to need to understand a bit more about how computation works under the hood.
The purpose of this article is to provide some fundamental background for computation. If there is interest I may follow up with some more advanced topics, but right now I want to look at the logic behind one of the simplest abstract computational devices–a finite state machine.
Finite State Machine
A finite state machine is a mathematical abstraction used to design algorithms. In simple terms, a state machine will read a series of inputs. When it reads an input it will switch to a different state. Each state specifies which state to switch for a given input. This sounds complicated but it is really quite simple.
Imagine a device that reads a long piece of paper. For every inch of paper there is a single letter printed on it–either the letter a or the letter b.
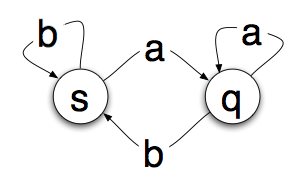
As the state machine reads each letter it changes state. Here is a very simple state machine.
The circles are “states” that the machine can be in. The arrows are the transitions. So if you are in state s and read an a you’ll transition to state q . If you read a b , you’ll stay in state s .
So if we start on s and read the paper tape above from left to right, we will read the a and move to state q . Then we’ll read a b and move back. Another b will keep us on s followed by an a which moves us back to the q state. Simple enough, but whats the point?
Well it turns out that you can run a tape through the state machine and once it is done tell something about the sequence of letters by examining the state you end up on. In our simple state machine above, if we end on s , the tape ends with the letter b , if we end on q , the tape ends with the letter a .
This may sound pointless, but there are an awful lot of problems that can be solved with this type of approach. A very simple example would be to determine if a page of HTML contains these tags in this order:
<html>
<head>
</head>
<body>
</body>
</html>
The state machine can move to state that shows it has read the html tag, loop until it gets to the head tag, loop until it gets to the head close tag, etc. If it successfully makes it to the final state, then you have those particular tags in the right order.
Finite state machines can also be used to represent the mechanics of a parking meter, pop machine, automated gas pump and all kinds of other things.
Deterministic Finite State Machine
The state machines we’ve looked at so far are all deterministic state machines. From any state there is only one transition for any allowed input. In other words there aren’t two paths leading out of a state when you read the letter a . At first this sounds silly to even make this distinction.
What good is a set of decisions if the same input can result in moving to more than one state? You can’t tell a computer, if x==true then execute doSomethingBig or execute doSomethingSmall, can you?
Well you kind of can with a state machine. The output of a state machine is its final state. It goes through all its processing and then the final state is read and then an action is taken. A state machine doesn’t do anything as it moves from state to state. It processes and then when it gets to the end, the state is read and something external triggers the desired action (dispenses a soda can, etc.). This is an important concept when it comes to non-deterministic finite state machines.
Non-deterministic Finite State Machine
Non-deterministic finite state machines are finite state machines where a given input from a particular state can lead to more than one different state. For example, lets say we want to build a finite state machine that can recognize strings of letters that start with a and are then followed by zero or more occurrences of the letter b or zero or more occurrences of the letter c terminated by the next letter of the alphabet. Valid strings would be:
- abbbbbbbbbc
- abbbc
- acccd
- acccccd
- ac (zero occurrences of b)
- ad (zero occurrences of c)
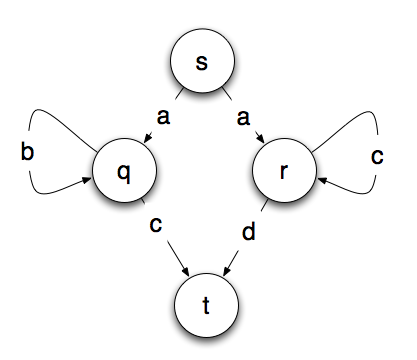
So it will recognize the letter a followed by zero or more of the same letter of b or c followed by the next letter of the alphabet. A very simple way to represent this is with a state machine that looks like the one below, where a final state of t means that the string was accepted and matches the pattern.
Do you see the problem? From starting point s, we don’t know which path to take. If we read the letter a , we don’t know whether to go to the state q or *r. * There are a few ways to solve this problem. One is by back tracking. You simply take all the possible paths and ignore or back out of the ones where you get stuck.
This is basically how most of the chess playing computers work. They look at all the possibilities and all the possibilities of those possibilities and choose the path that gives them the greatest number of advantages over their opponent.
The other option is to convert the non-deterministic machine into a deterministic machine. One of the interesting attributes of a non-deterministic machine is that there exists an algorithm to turn any non-deterministic machine into a deterministic one. However, it is often much more complicated. Fortunately for us, the example above is only slightly more complicated. In fact this one is simple enough we can transform it into a deterministic machine in our head without the aid of a formal algorithm.
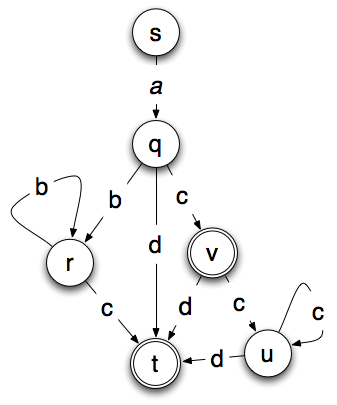
The machine below is a deterministic version of the non-deterministic machine above. In the machine below, a final state of t or *v * is reached by any string that is accepted by the machine.
The non-deterministic model has four states and six transitions. The deterministic model has 6 states, 10 transitions and two possible final states. That isn’t that much more, but the complexity usually grows exponentially and a moderately sized non-deterministic machine can produce an absolutely huge deterministic machine.
Regular Expression
If you have done any type of programming, you’ve probably encountered regular expressions. Regular expressions and finite state machines are functionally equivalent. Anything you can accept or match with a regular expression can be accepted or matched with a state machine. For example the pattern above could be matched with:
a(bc|cd)
Regular expressions and finite state machines also have the same limitations. In particular they both can only match or accept patterns that can be handled with finite memory. So what type of patterns can’t they match? Lets say you want to only match strings of a and b, where there are a number of a’s followed by an equal number of b’s. Or n a’s followed by n b’s where n is some number. Examples would be:
- ab
- aabb
- aaaaaabbbbbb
- aaaaaaaaaaaaaaaaaaaabbbbbbbbbbbbbbbbbbbb
At first this looks like an easy job for a finite state machine. The problem is that you’ll quickly run out of states or you’ll have to assume an infinite number of states–at which point it is no longer a finite state machine. Lets say you create a finite state machine that can accept up to 20 a’s followed by 20 b’s. That works fine until you get a string of 21 a’s followed by 21 b’s at which point you will need to rewrite your machine to handle a longer string. For any string you can recognize, there is one just a little bit longer that your machine can’t recognize because it runs out of memory.
This is known as the Pumping Lemma which basically says, if your pattern has a section that can be repeated like the one above then the pattern is not regular. In other words neither a regular expression nor a finite state machine can be constructed that will recognize all the strings that do match the pattern.
If you look carefully, you’ll notice that this type of pattern where every a has a matching b , looks very similar to HTML where within any pair of tags you may have any number of other matching pairs of tags. So while you may be able to use a regular expression or finite state machine to recognize if a page of HTML has the html , head and body elements in the correct order, you can’t use a regular expression to tell if an entire HTML page is valid or not because HTML is not a regular pattern.
Turing Machines
So how do you recognize non-regular patterns? There is a theoretical device that is similar to a state machine called a Turing Machine. It is similar to a finite state machine that it has a paper strip that it reads, but a Turing Machine can erase and write on the paper tape. Explaining a Turing Machine will take more space that we have here, but there are a few important points relevant to our discussion of finite state machines and regular expressions.
Turing Machines are computationally complete and anything that can be computed can be computed on a Turing Machine. Since a Turing Machine can write as well as read from the paper tape, it is not limited to a finite number of states. The paper tape can be assumed to be infinite in length. Obviously, actual computers don’t have an infinite amount of memory, but they contain enough memory that you don’t hit the limit for the type of problems they process.
Turing Machines give us an imaginary mechanical device that lets us visualize and understand how the computational process works. It is particularly useful in understanding the limits of computation. If there is interest I’ll do another article on Turing Machines in the future.
Why does this matter?
So whats the point? How is this going to help you create that next PHP form? Regardless of their limitations state machines are a very central concept to computing. In particular, the recognition that for any non-deterministic state machine you can design, there exists a deterministic state machine that does the same thing. This is a very key point because it means you can design your algorithm in whichever way is the easiest to think about. Once you have a proper algorithm, you can convert it into whatever form is most efficient.
The understanding that finite state machines and regular expressions are functionally equivalent opens up some incredibly interesting uses for regular expression engines–particularly when it comes to creating business rules that can be changed without recompiling a system.
A foundation in computer science allows you to take a problem X that you don’t know how to solve and reason, “I don’t know how to solve X, but I do know how to solve Y and I know how to convert a solution for Y into a solution for X. Therefore I now know how to solve X.”
(If you like this article, you might enjoy my YouTube channel where I create an occasional video or cartoon about some aspect of creating software. I also have a mailing list for people who would like an occasional email when I produce something new.)